Spreadsheets for
Analysis of Controlled Trials, with Adjustment for a Subject Characteristic Will G Hopkins Sportscience 10, 46-50, 2006
(sportsci.org/2006/wghcontrial.htm)
|
|
Update Dec 2007: See an In-brief item in the 2007 issue for a spreadsheet to analyze a post-only parallel-groups controlled trial. In 2003 and 2005 I published articles with links to spreadsheets for analysis of data from several kinds of controlled trial (Hopkins, 2003; Hopkins, 2005). The spreadsheets were designed for controlled trials that were simple in the sense that there was no provision for adjustment for a covariate (or predictor variable) in the analysis. The latest versions of the spreadsheets now address this problem by including one covariate. This article describes the development and use of the spreadsheets. Before you attempt to read the article and use the spreadsheets, make yourself familiar with the concepts I covered in the 2003 article and also with the concepts in the article on the various kinds of controlled trial (Batterham and Hopkins, 2005a). Why and How to
Include a Covariate
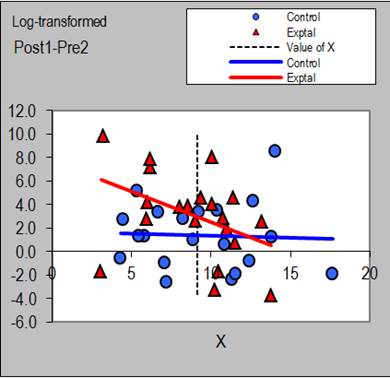
Including a covariate is important when, for reasons of poor randomization or drop-out of subjects, the experimental and control groups differ in the mean values of a subject characteristic such as age, fitness, or sex. In the absence of any adjustment, the difference between the groups in the effect of the treatment would be confounded by any interaction between the characteristic and the treatment. For example, if older subjects have a bigger response to the experimental treatment, and the experimental group is older than the control group, an analysis consisting only of a simple comparison of changes in the experimental and control groups will overestimate the magnitude of the effect for the average subject and younger subjects. When you include age in the analysis, you adjust the magnitude of the effect to the mean age of the subjects (or indeed to any age) and thereby remove the confounding effect. The adjustment is performed by fitting a simple linear model (a straight line) to the relationship between the change scores and the covariate in each group. The spreadsheet shows a plot for this relationship, and a vertical dashed line appears on the plot at the value of the covariate chosen for adjustment of the treatment effect (Figure 1).
The pre-test value of the dependent variable can also be included as a covariate to remove confounding arising from the phenomenon of regression to the mean, which can be a problem for dependent variables with measurement error that is appreciable relative to the differences between subjects. Any difference in the means of the groups in the pre-test will decrease on average in the post-test because of this phenomenon. Depending on the direction of the difference in the pre-test, the experimental effect will therefore be overestimated or underestimated. Including the pre-test value as a covariate corrects the problem. Even when there are no substantial differences in the mean value of a covariate between the groups, including the covariate in the analysis can be valuable. If the covariate turns out to have a substantial interaction with (have an effect on) the treatment, you will have accounted for individual differences in the effect of the treatment that would otherwise turn up as unexplained additional error of measurement in the experimental group. The precision of the estimate of the mean effect of the treatment will therefore be better when the covariate is included. The estimate of the effect of the covariate itself tells you how much the treatment effect differs between subjects with different values of the covariate. In the spreadsheets, you choose the amount of the difference in the covariate and the spreadsheet provides you with the corresponding difference in the treatment effect. For the correct qualitative interpretation of the magnitude of the effect of the covariate, you should choose two standard deviations' worth of the covariate. I explain why in a recent update of the page on magnitudes at my statistics site. The spreadsheets include a comment to prompt you for this value. If the covariate is a binary variable such as sex, code it as 0 and 1. Insert a value of 0 in the appropriate cell in the spreadsheet to get the effect for females, 1 to get the effect for males, and 0.5 to get the mean effect for females and males. Use the value 0.5 for the mean, even though there may be unequal numbers of males and females in the study. For the effect of sex itself, insert a value of 1 (the difference between females and males) in another appropriate cell. This method for dealing with a binary covariate is based on the assumption that the error variance is the same for the two groups represented by the covariate. An approach that avoids this assumption is to perform separate analyses for the two groups, then combine the outcomes using another spreadsheet designed partly for this purpose. See an article in this issue of Sportscience for a description of the spreadsheet and a link to it (Hopkins, 2006). In the article about the various kinds of controlled trials, Batterham and I called attention to the possibility of performing an analysis of a pre-post parallel-groups controlled trial using only the post-intervention values. Such analyses produce estimates with better precision when the dependent variable is sufficiently noisy. The new spreadsheets for the pre-post parallel-groups and pre-post crossover both work for these analyses. You simply put the post-intervention values rather than post-pre change scores in an effects column. The adjustment for the covariate also works with this approach, but for measures that aren't noisy the adjustment may not be as successful as in the usual pre-post analysis. Play with both approaches to find out what is going on with your data, and base your choice of analysis on better precision, not bigger effects (although the effects with better precision may be bigger). Estimates of individual responses will also work with such posts-only analyses, but you will need large sample sizes for anything like acceptable precision for the standard deviation representing the individual responses. Other
Enhancements
I have made other changes to the spreadsheets to enhance their user-friendliness, as follows: There are now plots of raw and back-transformed means against time or treatment. The standard-deviation bars in either direction can be removed simply. These plots require little extra tweaking for publication. The above plot for the analysis via log transformation has a log scale, so the standard-deviation bars are symmetrical about the mean and apply wherever they are placed along the Y axis. Excel's log scale works only in full decades, so for some data you will have to stretch the Y axis and trim off the excess in Powerpoint to get a figure for publication. See the In-Brief item on publication of high-resolution graphics in this issue of Sportscience for more tips about preparing figures. There is now a single cell for entering the smallest worthwhile standardized effect. The defaults are, of course, 0.2 and ‑0.2. These cells are linked to corresponding cells in the blocks of cells containing all the details of the inferences for the standardized effects. The blocks of cells containing inferences for raw and back-transformed variables now have a default smallest worthwhile effect calculated from the smallest standardized effect (bias-adjustedsee below), instead of the arbitrary numbers that were there before. You can choose a different value for the smallest worthwhile effect locally in each block of cells. Indeed, you must choose a different value when you are working with measures directly related to performance of athletes who compete as individuals, as I have pointed out in numerous publications (e.g., Hopkins, 2004). You can now choose one or more pretests to provide the standard deviation for calculation of standardized effects. The calculation for standardized effects now includes a correction for small-sample upward bias. I used a correction factor adapted from Becker (1988). The factor is 1-3/(4n-1), where n is the degrees of freedom of the standard deviation used to standardize the effect. This formula is more generic than those provided by Becker and better reflects the fact that the bias in the standardized effect arises solely from bias in the standard deviation. I checked the accuracy of the formula by performing some simple simulations in a spreadsheet, which you might find useful as an introduction to simulation with Excel. I have generated qualitative inferential outcomes based on interpretation of the span of the confidence interval relative to magnitude thresholds, as described by Batterham and Hopkins (2005b). If the span overlaps both the positive and the negative trivial-small thresholds, the outcome is shown as "unclear". Otherwise the outcome is shown as the qualitative magnitudes of the upper and lower confidence limits, separated by a dash. For standardized effects, the descriptors (and corresponding ranges of the standardized effect) are: very large ‑ive (less than ‑2.0), large ‑ive (‑2.0 to ‑1.2), moderate ‑ive (‑1.2 to ‑0.6), small ‑ive (‑0.6 to ‑0.2), trivial (‑0.2 to 0.2), small +ive (0.2 to 0.6), moderate +ive (0.6 to 1.2), large +ive (1.2 to 2.0), and very large +ive (more than 2.0). For all other effects, the descriptors are unclear, nontrivial ‑ive, trivial, and nontrivial +ive, as defined by the smallest worthwhile effect. There are now many new and sometimes lengthy comments in cells. Read and obey them to avoid problems, especially when you add or remove rows and columns. Limitations
The spreadsheets handle only one covariate at a time. Extending the analysis to two or more covariates is simple in theory, but it is practically impossible in Excel because of the bizarre awkwardness of the LINEST function (which performs the necessary multiple linear regression). Alas, there will be no update to two or more covariates in the foreseeable future. You can, however, include a binary covariate in addition to a continuous covariate by performing separate analyses for the two groups represented by the binary covariate, then combining them with another spreadsheet, as described earlier (Hopkins, 2006). There could be a fourth spreadsheet, for an uncontrolled time series. Meantime use the post-only crossover spreadsheet by replacing the treatment labels with values of time. You may have to insert more columns. When you have more than two treatment groups, you have to use a separate spreadsheet for each pairwise comparison of groups. You can also analyze each group separately using the post-only crossover spreadsheet as if the data were a time series, then compare the outcomes using the spreadsheet for combining outcomes from several groups, but this approach will not provide estimates of individual responses. The crossover spreadsheets do not adjust for any order effect in the crossover. Without adjustment, a substantial order effect degrades the precision of the estimate of the experimental effect. If there is also imbalance in the number of subjects doing the various orders of treatments, the treatment effect is confounded (biased) by the order effect. With two treatments, you can account for and estimate the order effect by performing separate analyses for the two groups of subjects (Treatment A first, Treatment B first), then combining the outcomes using the previously mentioned spreadsheet for combing independent effects. The mean of the two outcomes is free of the order effect; the difference (with the appropriate sign) is the order effect. With three or four treatments this approach is unwieldy but not out of the question. All these limitations and more are easily overcome with mixed modeling. Unfortunately none of the statistical packages that offer mixed modeling of sufficient complexity has an interface you can use successfully without a huge investment in time (years) and, for some, money ($10,000s). This problem applies to most analyses in all the statistical packages I have tried lately. See an In-brief item in this issue for more. The spreadsheets are not intended for binary outcome variables (win or lose, injured or not, etc.). Such variables need generalized linear modeling, which apparently can be performed using the Solver in Excel. I am looking into it. The confidence limits for standardized effects are approximate, because the sampling distribution on which they are based (the t distribution) does not take into account uncertainty in the standard deviation used to perform the standardizing. In the special case of degrees of freedom of the unstandardized effect being the same as that for the standard deviation, the required sampling distribution is a non-central t, functions for which are available as a third-party macro. I have compared the confidence limits produced by the usual t and non-central t. Those from the usual t are further from the mean at the lower limit, so the inferences in the spreadsheets for the standardized effects are conservative. In any case, the discrepancies are negligible for sample sizes of 10 or more. I generated data shown in the spreadsheets with known population effects using NORMSINV(RAND()) in an Excel spreadsheet. This spreadsheet will be the basis of an article on teaching statistics with simulation, which I hope to publish in the next issue of Sportscience. I also wrote a program using Proc Mixed in SAS to check the analysis of mean effects and individual responses. This zip file contains the data, the SAS program, and the resulting listing. Making the text and comments specific to each kind of analysis in the three spreadsheets was a challenging exercise that I won't have completed without errors. Please contact me with any corrections. Statistical Basis
for the Spreadsheets
To incorporate a covariate into the spreadsheets, I had to change the way the inferential statistics were calculated. Previously I used Excel's TTEST function to generate a p value for the comparison of the groups, then converted the p value into a standard error and thence into confidence limits and chances that the true effect was substantial in a positive and negative sense. For the new spreadsheets I used well-established formulae to calculate the standard errors of the mean change scores, of the regression-predicted change scores, and of the slope of the covariate. I calculated separate standard errors in this way for the experimental and control groups, then combined them to get the standard error of the between-group difference of each of these three statistics. For the pre-post parallel-groups spreadsheet, the groups are independent, so the standard error for the difference is simply the square root of the sum of the squares of the two standard errors, with degrees of freedom given by the well-known Satterthwaite approximation that is the basis for the unequal-variances unpaired t test (Satterthwaite, 1946). For the pre-post crossover, the two groups are the same subjects, so I had to adjust the standard error using a first-principles formula involving the correlation between the groups: SEE-C2 = SEE2 + SEC2 - 2rEC.SEE.SEC, References
Batterham AM, Hopkins WG (2005a). A decision tree for controlled trials. Sportscience 9, 33-39 Batterham AM, Hopkins WG (2005b). Making meaningful inferences about magnitudes. Sportscience 9, 6-13 Becker BJ (1988). Synthesizing standardized mean-change measures. British Journal of Mathematical and Statistical Psychology 41, 257-278 Hopkins WG (2003). A spreadsheet for analysis of straightforward controlled trials. Sportscience 7, sportsci.org/jour/03/wghtrials.htm (4447 words) Hopkins WG (2004). How to interpret changes in an athletic performance test. Sportscience 8, 1-7 Hopkins WG (2005). A spreadsheet for fully controlled crossovers. Sportscience 9, 24 Hopkins WG (2006). A spreadsheet for combining outcomes from several subject groups. Sportscience 10, 51-53 Satterthwaite FW (1946). An approximate distribution of estimates of variance components. Biometrics Bulletin 2, 110-114 Published Dec 2006 |