Bootstrapping Inferential Statistics with a Spreadsheet Will G Hopkins Sportscience 16, 12-15, 2012 (sportsci.org/2012/wghboot.htm) Sport and Recreation, AUT University, Auckland 0627, New
Zealand. Email.
Reviewer: Alan M Batterham, School of Health and Social Care, University of
Teesside, Middlesbrough TS1 3BA, UK. |
|
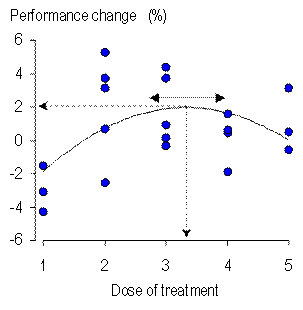
When you analyze the data from the study of a sample, you have to estimate the uncertainty in the magnitude of an effect representing the relationship between predictor and dependent variables. Uncertainty refers to the fact that a different sample would give a different value for the magnitude. The uncertainty should be expressed as confidence limits or a confidence interval, representing the range of values within which you are reasonably certain the true magnitude of the relationship would fall. True refers to the value you would get if you had the luxury of a huge sample, and reasonably certain is the level of confidence, such as 90% or 99%. You should also calculate the probabilities that the true effect is substantial in some positive and negative sense. The confidence limits and probabilities are inferential statistics that help you make a probabilistic decision about the magnitude of the true effect (Hopkins et al., 2009). Fine, so how do you calculate the confidence limits and the probabilities? The usual approach is to make assumptions about the way the value of the effect statistics would vary, if you repeated the study again and again. The values make up the so-called sampling distribution of the statistic. For many statistics the shape of the sampling distribution is known, and the confidence limits and probabilities can be worked out using well-known formulae involving the t or related statistics derived from the sample. These formulae are the basis of the inferences built into the spreadsheets at this site. Bootstrapping is an alternative approach to generating confidence limits and probabilities about the true value of the effect, and it is the only approach when the sampling distribution is either not known or too difficult to quantify. In the item on bootstrapping at my stats site, I give the example of the difference between correlation coefficients derived from the same subjects. Another example that has emerged in several studies with my colleagues is the optimum value of a predictor that has a quadratic relationship with the dependent variable. Figure 1 shows an example where the predictor is dose of a treatment and the dependent is change in performance. Similar quadratic relationships work well for modeling the optimum age in an athlete's career performance trajectory (unpublished observations). Indeed, it is a simple matter to show with calculus that the relationship between any predictor and dependent in the vicinity of a maximum or a minimum is quadratic. A quadratic model is therefore an important analytical tool for investigating optima. Conventional modeling can provide approximate confidence limits for the optimum value of the dependent, but exact confidence limits for the optimum and for the value of the dependent evincing it require bootstrapping.
The term bootstrapping refers to the old paradox about people lifting themselves off the ground by pulling up on the straps on the backs of their own boots. A similar seemingly impossible thing occurs when you resample (to describe bootstrapping more formally) to get confidence limits. Here's how it's done. For a sample of 20 or more subjects drawn randomly from some population, you can "sort of" recreate the population by duplicating the sample endlessly. The next step is to draw at least 1000 samples from this population, each of the same size as the original sample. In any given sample, some subjects will appear twice or more, while others won't be there at all, but that doesn't matter. Next you calculate the values of the outcome statistics for each of these samples. In the example above, the statistics would be the value of dose at the maximum, given by x = ‑b/2a for the quadratic y = ax2+bx+c, along with the value of performance change when this value of x is put into the quadratic. Finally, you rank the resulting 1000 values of the optimum dose and count in from each end until you reach the 5th percentile and 95th percentile, which are the 90% confidence limits. The PERCENTILE function in Excel provides the estimates without sorting and ranking the values. You repeat this process for the effect on the dependent variable (here, performance change) at the optimum. The median value (50th percentile) from the bootstrap samples should be practically the same as the value of the outcome statistic in the original sample. A slight mismatch can occur with only 1000 bootstrap samples. I have not used more samples, because the files are already quite large (2-3 MB), and the calculations can be slow to update. When you refresh the bootstrap samples (using Ctrl-D–see instructions in the spreadsheet), the median should hover around the original value. A consistent substantial difference can arise when the dependent and/or predictor variables are skewed, in which case log transformation may correct the problem. A predictor variable with only a few integer values (e.g., 0 and 1, denoting females and males) can also result in a consistent mismatch, especially if most of the values of the predictor are the same (e.g., 17 males denoted by 1s and only 3 females denoted by 0s). If something like this in your data produces a big difference, the only solution is a larger sample size than in your original study, which is usually out of the question by the time you are doing the analysis. The links below point to four spreadsheets. I suggest you work your way through them in the order shown. Start with the simplest of all linear models, a single predictor. Try changing the values of the predictor to 0s and 1s to model the simple difference in the means between two groups. (Note that bootstrapping automatically takes into account any difference in the standard deviations in the two groups, which you would normally deal with using the unequal-variances t statistic.) Move on to the spreadsheet for a quadratic predictor. You will find this spreadsheet allows for a quadratic maximum (an inverted-U shape) and a quadratic minimum (a U shape). If the quadratic effect is weak and the sample size is not large, a substantial proportion of the bootstrap samples will have a shape opposite to that of the original sample, in which case you will have to abandon quadratic modeling and opt instead for a simple linear model (using either the previous spreadsheet or usual modeling). The third spreadsheet has a quadratic model with adjustment for the effect of an extra linear covariate. The covariate can be continuous or scored simply as 0s and 1s, as shown in the spreadsheet. Note, however, that the model fits a quadratic of the same shape to the two groups of subjects implied by the 0s and 1s. If you want to fit a different quadratic to two or more groups, put each group into a separate spreadsheet, hopefully with 20 subjects in each group! You can do inferential comparisons of the resulting statistics for the groups using the spreadsheet to compare/combine effects (Hopkins, 2006). The last spreadsheet has two linear predictors. Use this one if quadratic modeling with the third spreadsheet fails. For all their complexity, these spreadsheets lack several features of my other spreadsheets: log transformation, standardization of effects, and qualitative inferences… • You will need to do any necessary log transformation before entering the numbers in the bootstrap spreadsheet. If your data represent a change in performance (as shown in the spreadsheets) and the effects are more than a few percent, you should enter the change in 100× the natural log of the performance scores, not the actual percent changes. Back-transform the bootstrapped effect on performance to a percent score using the formula 100*exp(effect/100)-100. (For effects of <10%, there is practically no difference between the 100×natural-log and the back-transformed effects.) • Standardization is performed by dividing all effects by the appropriate between-subject standard deviation. If you used log transformation, do the standardization entirely with log-transformed values, including the standard deviation of the log-transformed raw data. • The spreadsheets provide estimates of chances that the true effects are substantial and the odds ratios for substantially positive/negative, but you will have to understand the process of magnitude-based inference to convert these to qualitative inferences (unclear, possibly negative, likely beneficial, etc.). See the appropriate section of the progressive statistics article (Hopkins et al., 2009) for more. Finally, how the spreadsheets work… I use the LINEST function to do a multiple linear regression connecting the predictors to the dependent. LINEST has several annoying "features": you have to invoke it with a strange combination of keystrokes, you can't have missing values, you can't insert columns, and (unbelievably) the coefficients of the predictors are produced in the opposite order to the variables. LINEST also produces standard errors but not covariances for the coefficients, so you can't use it to estimate confidence limits for predicted values. (Bootstrapping generates confidence limits without using the standard errors.) See the link below for separate instructions on how to use LINEST. Bootstrapping is a lot easier with Excel since the advent of xlsx files, because each bootstrap sample occupies several columns, and xls files were limited to 256 columns. For each bootstrap sample I create a set of columns that are copies of the columns where the original data are analyzed. The data for each bootstrap sample are selected from the original data using the RANDBETWEEN and INDEX functions, as you will see if you click on the appropriate cells. It's then a simple matter to generate the confidence limits and probabilities of exceeding magnitude thresholds using the PERCENTILE function. SpreadsheetsA single linear predictor: Bootstrap1predictor.xlsx A quadratic predictor: BootstrapQuadratic.xlsx A quadratic plus a linear covariate: BootstrapQuadraticPlus1covariate.xlsx Two linear predictors: Bootstrap2predictors.xlsx How to use LINEST: UsingLINESTinExcel.xlsx ReferencesPublished July 2012 |