|
A New View of Statistics | |
A percent error in a variable is actually a multiplicative factor. For example, an error of 5% means the error is typically 5/100 times the value of the variable. When you take logs, the multiplicative factor becomes an additive factor, because that's how logs work: log(Y*error) = log(Y) + log(error). The percent error therefore becomes the same additive error, regardless of the value of Y. So your analyses work, because your non-uniform residuals become uniform. This feature of log transformation is useful for analysis of most types of athletic performance and many other measurements on humans.
Percent Effects from Log-Transformed
Variables
If the percent error in a variable is similar from
subject to subject, it's likely that treatment effects or differences between
groups expressed as percents are also similar from subject to subject. It therefore
makes sense to express a change or difference as a percent rather than as a
raw number. For example, it's better to report the effect of a drug treatment
on high-jump performance as 4% rather than 8 cm, because the drug affects every
athlete by 4%, but only those athletes who jump 2 m will experience a change
of 8 cm. In such situations, the analysis of the log-transformed variable provides
the most accurate estimate of the percent change or difference. Make sure you
use natural logs, not base-10 logs, then analyze the log-transformed variable
in the usual way.
Suppose you end up with a difference of 0.037 (you'll often get small numbers like this).
|
Explanation of 100(ediff - 1) and 100diff |
| If Z = log(Y) and Z' = log(Y'), then diff = Z' - Z = log(Y') - log(Y) = log(Y'/Y). But Y'/Y = 1+(Y'-Y)/Y = 1+(percent change in Y)/100. Therefore ediff = Y'/Y = 1+(percent change in Y)/100. Therefore percent change in Y = 100(ediff - 1). For small diff, ediff = 1 + diff, so percent change in Y is approximately 100diff. |
I find it easier to interpret the diffs (differences or changes) in a log-transformed variable if I use 100x the log of the variable as the log transformation. That way the diffs are already approximately percents. For example, instead of getting a change of 0.037, you will get 3.7, which means approximately 3.7%. To convert this diff to an exact percent, the formula is 100(ediff/100 - 1), obviously! A diff of 3.7 is really 100(e3.7/100 - 1) = 3.8%.
It's easy to get confused when the percent change is large. For example, a change of 90% means that the final value is (1 + 90/100) or 1.90 times the initial value. A change of 100% therefore means that the final value is (1 + 100/100) or 2.0 times the initial value. A 200% increase means that the value has increased by a factor of 3, and so on. A negative percent change can also be confusing. (In a previous version of this paragraph, my interpretation of large negative changes was wrong!) A change of -43% means that the final value is (1 - 43/100) or 0.57 times the initial value. An 80% fall means that the final value is only 0.20 times the initial value, and so on.
When variables need log transformation to make them normal, how do you represent their means and standard deviations? I think a hybrid approach is best. Convert the mean of the log-transformed variable back to raw units using the back-transformation Y = emean (if your transformation was Z = logY) or Y = emean/100 (if you used Z = 100logY). Keep the standard deviation as a percent variation or coefficient of variation (CV). Calculate this CV in the same way as for differences or changes in the variable: if SD is the standard deviation of the log-transformed variable, the approximate CV is simply 100SD, and the exact CV is 100(eSD - 1). If you used 100log for your transformation, the approximate CV is simply the SD itself, and the exact CV is 100(eSD/100 - 1).
You can convert the CV into a raw standard deviation, but it's messy and I don't recommend it. Back-transforming the SD as eSD is incorrect. Instead, you have to show the upper and lower values of the mean ± standard deviation as emean + SD and emean - SD. With a bit of algebra, you can show that emean + SD is equal to the back-transformed mean times 1 + CV, and emean - SD is the back-transformed mean times 1/(1 + CV). Hence a CV of, say, 23% represents a typical variation in the mean of ×1.23 through ×1/1.23. As I explain on the page about calculating reliability as a CV, it's OK to write ±CV, provide you realize what it really means.
CAUTION. With log and other non-linear transformations, the back-transformed mean of the transformed variable will never be the same as the mean of the original raw variable. Log transformation yields the so-called geometric mean of the variable, which isn't easily interpreted. Rank transformation yields the median, or the middle value, which at least means something you can understand. The square-root and arcsine-root transformations for counts and proportions yield goodness-knows-what. Usually it's the effects you are interested in, not the mean values for groups, so you don't need to worry. But if the means are important, for example if you want the true mean counts of injuries to come out of your analysis, you will have to use a cutting-edge modeling approach that does not require transformation, such as binomial regression.
If you're graphing means and standard deviations of a variable that needed log transformation, use a log scale on the axis. Here's how. Plot the values you get from the log-transformed data without back-transformation, but delete the tick marks and put new ticks corresponding to values of the original raw variable that you would normally show on a plot. (You will struggle to understand what I am getting at here. Persevere. And if you use Excel to do your graphs, paste the graph into Powerpoint and do the editing there.) The error bar or bars go onto the plot without and fiddling. In fact, you can put the error bar anywhere on the axis.
More Examples of Log Transformation
|
|
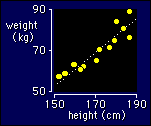
Many relationships that have a curve in them respond well to log-log transformation. To get technical, all models of the form Y = aXn convert to simple linear models when you take logs: logy = loga + nlogX. The relationship between weight (Y) and height (X) is a particularly good example. The value of the parameter n is given by the slope of the log-log plot, and it is about 1.7, or nearly 2, which is why we normalize body weights by dividing by the height squared to get the so-called body mass index. It would be better to divide by height to the power of 1.7, but that's another story.
|
|